Упражнение 1.
Используя рисунок 139, докажите, что изображение точки расположено за зеркалом на таком же расстоянии, на каком точка находится перед зеркалом.
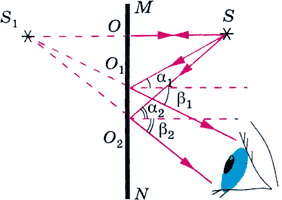
`{(∠S_1O_2O = 180° - ∠S_1OO_2 - ∠OS_1O_2),(∠OS_1O_2 = ∠β_2),(∠SOO_1 = ∠S_1OO_2 = 90°):}`
`∠S_1O_2O = 90° - ∠β_2`
`{(∠SO_2O = 90° - ∠α_2),(∠α_2 = ∠β_2):}`
`∠SO_2O = 90° - ∠β_2`
Рассмотрим `ΔS_1OO_2` и `ΔOSO_2`.
`∠S_1O_2O = ∠SO_2O`, `∠SOO_2 = ∠S_1OO_2`, сторона `OO_2` общая `rArr` `ΔS_1OO_2` равен `ΔOSO_2`.
Из равенства треугольников следует, что `S_1O = OS`.
Вывод: изображение точки расположено за зеркалом на таком же расстоянии, на каком точка находится перед зеркалом.